[原创]高等数学笔记(14)

【前言】
请看此文。
要查看高等数学笔记合集，请看这里。

【正文】
例3. 求 $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 1}}{{x - 1}}$

解：
$\mathop {\lim }\limits_{x \to 1} (x - 1) = \mathop {\lim }\limits_{x \to 1} x - 1 = 1 - 1 = 0$
$\mathop {\lim }\limits_{x \to 1} ({x^2} + 1) = {\left[ {\mathop {\lim }\limits_{x \to 1} x} \right]^2} + 1 = 2 \ne 0$
因为 $\mathop {\lim }\limits_{x \to 1} \frac{1}{{\frac{{{x^2} + 1}}{{x - 1}}}} = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{{x^2} + 1}} = \frac{{\mathop {\lim }\limits_{x \to 1} (x - 1)}}{{\mathop {\lim }\limits_{x \to 1} ({x^2} + 1)}} = \frac{0}{2} = 0$
所以当 $x \to 1$ 时， $\frac{1}{{\frac{{{x^2} + 1}}{{x - 1}}}}$ 是无穷小
由无穷小与无穷大的关系（无穷小的倒数是无穷大），可知 $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} + 1}}{{x - 1}} = \infty$
文章来源：http://www.codelast.com/
例4. 求 $\mathop {\lim }\limits_{x \to 1} \left( {\frac{1}{{x - 1}} - \frac{2}{{{x^2} - 1}}} \right)$
解：
当 $x \to 1$ 时， $\frac{1}{{x - 1}} \to \infty ,\;\frac{2}{{{x^2} - 1}} \to \infty$
所以不能直接用极限的四则运算公式来计算。
$\mathop {\lim }\limits_{x \to 1} \left( {\frac{1}{{x - 1}} - \frac{2}{{{x^2} - 1}}} \right) = \mathop {\lim }\limits_{x \to 1} \frac{{x + 1 - 2}}{{{x^2} - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{{x^2} - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{x - 1}}{{(x - 1)(x + 1)}} = \mathop {\lim }\limits_{x \to 1} \frac{1}{{x + 1}} = \frac{1}{2}$

例5. 求 $\mathop {\lim }\limits_{x \to \infty } \frac{{2{x^2} + 5x + 1}}{{{x^2} - 4x - 8}}$
解：
分子、分母同时除以 ${{x^2}}$ （选分子多项式及分母多项式中最高的次数），得：
原式 $= \mathop {\lim }\limits_{x \to \infty } \frac{{2 + \frac{5}{x} + \frac{1}{{{x^2}}}}}{{1 - \frac{4}{x} - \frac{8}{{{x^2}}}}} = \frac{{\mathop {\lim }\limits_{x \to \infty } 2 + 5\mathop {\lim }\limits_{x \to \infty } \frac{1}{x} + {{\left( {\mathop {\lim }\limits_{x \to \infty } \frac{1}{x}} \right)}^2}}}{{\mathop {\lim }\limits_{x \to \infty } 1 - 4\mathop {\lim }\limits_{x \to \infty } \frac{1}{x} - 8{{\left( {\mathop {\lim }\limits_{x \to \infty } \frac{1}{x}} \right)}^2}}} = \frac{{2 + 0 + 0}}{{1 - 0 - 0}} = 2$
文章来源：http://www.codelast.com/

一、准则1：夹挤准则
若在 $N({x_0},{\delta _0})$ 内（ ${\delta _0} > 0$ ），有 $F(x) \le f(x) \le G(x)$ 成立，而且 $\mathop {\lim }\limits_{x \to {x_0}} F(x) = \mathop {\lim }\limits_{x \to {x_0}} G(x) = A$ ，则 $\mathop {\lim }\limits_{x \to {x_0}} f(x)$ )存在，且极限值为 $A$ 。以上结论对 $x \to \infty$ 也成立。
证：
因为 $\mathop {\lim }\limits_{x \to {x_0}} F(x) = A$
所以对 $\forall \varepsilon > 0$ ，必 $\exists {\delta _1} > 0$ ，使得适合不等式 $0 < \left| {x - {x_0}} \right| < {\delta _1}$ 的一切 $x$ 所对应的 $F(x)$ ，恒有 $\left| {F(x) - A} \right| < \varepsilon$

因为 $\mathop {\lim }\limits_{x \to {x_0}} G(x) = A$
所以对 $\forall \varepsilon > 0$ ，必 $\exists {\delta _2} > 0$ ，使得适合不等式 $0 < \left| {x - {x_0}} \right| < {\delta _2}$ 的一切 $x$ 所对应的 $G(x)$ ，恒有 $\left| {G(x) - A} \right| < \varepsilon$
现取 $\delta = \min \left\{ {{\delta _0},{\delta _1},{\delta _2}} \right\}$ ，则适合不等式 $0 < \left| {x - {x_0}} \right| < \delta$ 的一切 $x$ 所对应的 $F(x),f(x),G(x)$ 都满足 $F(x) \le f(x) \le G(x)$
文章来源：http://www.codelast.com/
由上面推导出来的：
$\left| {F(x) - A} \right| < \varepsilon \Leftrightarrow A - \varepsilon < F(x) < A + \varepsilon$
$\left| {G(x) - A} \right| < \varepsilon \Leftrightarrow A - \varepsilon < G(x) < A + \varepsilon$
$\Rightarrow A - \varepsilon < F(x) \le f(x) \le G(x) < A + \varepsilon \Rightarrow A - \varepsilon < f(x) < A + \varepsilon \Leftrightarrow \left| {f(x) - A} \right| < \varepsilon$
根据极限定义，有 $\mathop {\lim }\limits_{x \to {x_0}} f(x) = A$

例1. 证明 $\mathop {\lim }\limits_{\alpha \to 0} \sin \alpha = 0,\;\mathop {\lim }\limits_{\alpha \to 0} \cos \alpha = 1$
证：
利用单位圆来找不等式（夹挤准则）两端的函数（如下图所示）。

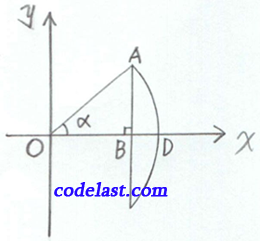
先证 $\mathop {\lim }\limits_{\alpha \to 0} \sin \alpha = 0$
作单位圆（圆心在原点 $O$ ）
$0 < \alpha < \frac{\pi }{2}$ （角度用弧度来表示）
圆心角 $\alpha$ 对应的圆弧长度 $\stackrel \frown {AD} = 1 \cdot \alpha = \alpha$ （圆弧长度=半径×角的弧度）
由直角三角形 $AOB$ 可知 $\frac{{AB}}{{AO}} = \frac{{AB}}{1} = AB = \sin \alpha$
因为 $0 < AB < \stackrel \frown {AD}$
所以 $0 < \sin \alpha < \alpha$
又因为 $\mathop {\lim }\limits_{\alpha \to {0^ + }} 0 = 0$ （常数的极限为0）， $\mathop {\lim }\limits_{\alpha \to {0^ + }} \alpha = 0$
所以根据夹挤准则可知 $\mathop {\lim }\limits_{\alpha \to {0^ + }} \sin \alpha = 0$
文章来源：http://www.codelast.com/
以上求出了右极限，下面求左极限。
若 $- \frac{\pi }{2} < \alpha < 0$ ，令 $t = - \alpha$
当 $\alpha \to {0^ - }$ 时， $t \to {0^ + }$
$\mathop {\lim }\limits_{\alpha \to {0^ - }} \sin \alpha = \mathop {\lim }\limits_{t \to {0^ + }} \sin ( - t) = - \mathop {\lim }\limits_{t \to {0^ + }} \sin t = 0$
即 $\mathop {\lim }\limits_{\alpha \to {0^ + }} \sin \alpha = \mathop {\lim }\limits_{\alpha \to {0^ - }} \sin \alpha = 0$ （左、右极限均存在且相等）
所以 $\mathop {\lim }\limits_{\alpha \to 0} \sin \alpha = 0$
文章来源：http://www.codelast.com/
再证 $\mathop {\lim }\limits_{\alpha \to 0} \cos \alpha = 0$
在直角 $\bigtriangleup AOB$ 中， $OA - AB < OB < 1$ （三角形两边之差小于第三边）
所以 $1 - AB < OB < 1$
$AB = \sin \alpha ,\;OB = \cos \alpha$
$1 - \sin \alpha < \cos \alpha < 1$
$\mathop {\lim }\limits_{\alpha \to 0} (1 - \sin \alpha ) = 1 - \mathop {\lim }\limits_{\alpha \to 0} \sin \alpha = 1 - 0 = 1$
由夹挤准则可知 $\mathop {\lim }\limits_{\alpha \to 0} \cos \alpha = 1$
文章来源：http://www.codelast.com/
（第14课完）

文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤ 
转载需注明出处：codelast.com 
感谢关注我的微信公众号（微信扫一扫）：