【正文】
四、连续函数在闭区间上的性质
函数在区间  上的最大、最小值定义:
上的最大、最小值定义:
设函数  在区间
在区间  上有定义,如果
上有定义,如果  ,使得
,使得  ,都有
,都有  (或
(或  ),则称
),则称  是
是  在区间
在区间  上的最小值(或
上的最小值(或  是
是  在
在  上的最大值),记为:
上的最大值),记为:
 (或
(或  )
)
文章来源:http://www.codelast.com/
1.最大、最小值定理
闭区间上的连续函数在该区间上一定有最大值和最小值,即:若  在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续(记为
上连续(记为 ![f(x) \in C\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ba93de316066f816c78689ba199596e5.gif) ),则必定存在
),则必定存在 ![\xi ,\eta \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_0c65b83bbaf4a04c6761334cb36ecbf0.gif) ,使得:
,使得:
![\mathop {\min }\limits_{x \in [a,b]} f(x) = f(\xi ),\;\mathop {\max }\limits_{x \in [a,b]} f(x) = f(\eta )](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ed63fd4b0fce502c47b4c1e09e77b213.gif)
即: ![f(\xi ) \le f(x) \le f(\eta ),\;x \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_1cf6f3c757755764d6f9d322cad6b7e3.gif)
注意:“闭区间”、“连续”这两个条件不可少。
文章来源:http://www.codelast.com/
例如:  在
在  连续,但它既无最大值,也无最小值。
连续,但它既无最大值,也无最小值。
又如:

函数图像如下图所示:
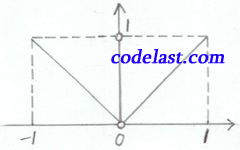
 在
在 ![[ - 1,1]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_31850cc60ee37802008d73c9a46bf5ba.gif) 上的
上的  点处不连续,
点处不连续,  在
在 ![[ - 1,1]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_31850cc60ee37802008d73c9a46bf5ba.gif) 内无最小值。
内无最小值。文章来源:http://www.codelast.com/
2.有界性定理
在闭区间上连续的函数在该区间上一定有界。
证:设
 在闭区间
在闭区间 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续,由性质1(最大、最小值定理)可知:一定存在最大值
上连续,由性质1(最大、最小值定理)可知:一定存在最大值  和最小值
和最小值  ,使
,使 ![m \le f(x) \le M,\;x \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_131da8bf97d400ce5fae29424c3a0764.gif)
所以
 在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上既有上界,也有下界
上既有上界,也有下界  在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上有界。
上有界。文章来源:http://www.codelast.com/
3.零值点定理
使函数
 的函数值等于0的点
的函数值等于0的点  (即
(即  )称为
)称为  的零值点。
的零值点。设
 在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续,且
上连续,且  与
与  异号(即
异号(即  ),则至少存在一点
),则至少存在一点  ,使
,使  。
。若
 在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续,则函数曲线
上连续,则函数曲线  是连续曲线,两端点为
是连续曲线,两端点为  。
。因为
 异号,点
异号,点  在
在  轴上、下两侧,连接
轴上、下两侧,连接  的连续曲线必定与
的连续曲线必定与  轴相交,此交点即为
轴相交,此交点即为  的零值点。
的零值点。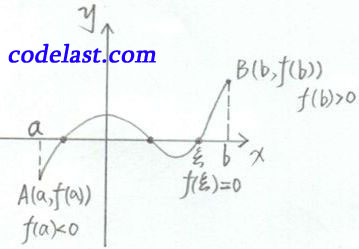
4.介值定理
设![f(x) \in C\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ba93de316066f816c78689ba199596e5.gif) (即在
(即在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续),且
上连续),且  ,则对于数
,则对于数  (
(  介于
介于  之间),则至少存在一点
之间),则至少存在一点  ,使
,使  。
。
证:
不妨设 ,即
,即 
作函数 在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续(两个连续函数的差是连续的)
上连续(两个连续函数的差是连续的)


所以 异号
异号
所以由结论3可得结论4。
文章来源:http://www.codelast.com/
推论:设![f(x) \in C\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ba93de316066f816c78689ba199596e5.gif) ,令
,令 ![m = \mathop {\min }\limits_{x \in [a,b]} f(x),M = \mathop {\max }\limits_{x \in [a,b]} f(x)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_a283470e99641f08365277e7e8e6a6c2.gif) ,则
,则  ,而数
,而数  ,则至少存在一点
,则至少存在一点  ,使
,使 
证:
由性质1可知,至少存在点![{x_1},{x_2} \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_aebba76d44678c32f1298e7614a9c416.gif) ,使
,使 
则函数 在
在 ![[{x_1},{x_2}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8127e83094f96dcb9c1e14d94f2e7bd6.gif) 或
或 ![[{x_2},{x_1}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8276bf9d48218eeeecf6d78c627aeff8.gif) 上是连续的(注:因为不知道
上是连续的(注:因为不知道  谁大谁小,所以有两种情况)
谁大谁小,所以有两种情况)
在![[{x_1},{x_2}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8127e83094f96dcb9c1e14d94f2e7bd6.gif) 或
或 ![[{x_2},{x_1}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8276bf9d48218eeeecf6d78c627aeff8.gif) 上利用性质4即得结论。
上利用性质4即得结论。
文章来源:http://www.codelast.com/
例1. 设 (即
(即  在开区间
在开区间  内连续),
内连续),  ,请证明:至少存在一点
,请证明:至少存在一点  ,使得
,使得 
证:
令
则![[c,d] \subset (a,b)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_634507284d01409239f5af1ad8301f06.gif) ,且
,且 ![f(x) \in C\left[ {c,d} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_68a8d7c606584935e8903dc9ef2c7ef6.gif)
由性质1可知,一定存在![m = \mathop {\min }\limits_{x \in [c,d]} f(x),M = \mathop {\max }\limits_{x \in [c,d]} f(x)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7b25e8649af05a8e9122d0e38cba3db3.gif)
从而有
n个不等式相加:


由性质4推论即得结论成立:至少存在一点![\xi \in [c,d] \subset (a,b)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_d8336f9a0f306955123ff5bdd6bb6964.gif) ,使
,使 
文章来源:http://www.codelast.com/
(第21课完)
设
![f(x) \in C\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ba93de316066f816c78689ba199596e5.gif) (即在
(即在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续),且
上连续),且  ,则对于数
,则对于数  (
(  介于
介于  之间),则至少存在一点
之间),则至少存在一点  ,使
,使  。
。证:
不妨设
 ,即
,即 
作函数
 在
在 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上连续(两个连续函数的差是连续的)
上连续(两个连续函数的差是连续的)

所以
 异号
异号所以由结论3可得结论4。
文章来源:http://www.codelast.com/
推论:设
![f(x) \in C\left[ {a,b} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ba93de316066f816c78689ba199596e5.gif) ,令
,令 ![m = \mathop {\min }\limits_{x \in [a,b]} f(x),M = \mathop {\max }\limits_{x \in [a,b]} f(x)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_a283470e99641f08365277e7e8e6a6c2.gif) ,则
,则  ,而数
,而数  ,则至少存在一点
,则至少存在一点  ,使
,使 
证:
由性质1可知,至少存在点
![{x_1},{x_2} \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_aebba76d44678c32f1298e7614a9c416.gif) ,使
,使 
则函数
 在
在 ![[{x_1},{x_2}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8127e83094f96dcb9c1e14d94f2e7bd6.gif) 或
或 ![[{x_2},{x_1}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8276bf9d48218eeeecf6d78c627aeff8.gif) 上是连续的(注:因为不知道
上是连续的(注:因为不知道  谁大谁小,所以有两种情况)
谁大谁小,所以有两种情况)在
![[{x_1},{x_2}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8127e83094f96dcb9c1e14d94f2e7bd6.gif) 或
或 ![[{x_2},{x_1}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8276bf9d48218eeeecf6d78c627aeff8.gif) 上利用性质4即得结论。
上利用性质4即得结论。文章来源:http://www.codelast.com/
例1. 设
 (即
(即  在开区间
在开区间  内连续),
内连续),  ,请证明:至少存在一点
,请证明:至少存在一点  ,使得
,使得 
证:
令

则
![[c,d] \subset (a,b)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_634507284d01409239f5af1ad8301f06.gif) ,且
,且 ![f(x) \in C\left[ {c,d} \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_68a8d7c606584935e8903dc9ef2c7ef6.gif)
由性质1可知,一定存在
![m = \mathop {\min }\limits_{x \in [c,d]} f(x),M = \mathop {\max }\limits_{x \in [c,d]} f(x)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7b25e8649af05a8e9122d0e38cba3db3.gif)
从而有

n个不等式相加:


由性质4推论即得结论成立:至少存在一点
![\xi \in [c,d] \subset (a,b)](https://www.codelast.com/wp-content/plugins/latex/cache/tex_d8336f9a0f306955123ff5bdd6bb6964.gif) ,使
,使 
文章来源:http://www.codelast.com/
(第21课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
