很多最优化算法需要用到一维搜索(line search)子算法,而在众多的一维搜索算法中,大多数都要求函数被限制在一个单峰区间内,也就是说,在进行一维搜索的区间内,函数是一个单峰函数。尽管有一些改进的一维搜索算法(例如  建议的一种改进过的黄金搜索算法)可以处理函数非单峰的情况,但是,在没有确定函数在一个区间内是单峰的之前,即使在搜索过程中,函数值持续减小,我们也不能说极小值是一定存在的,因此,找出一个区间,在此区间之内使函数是单峰的,这个过程是必需的(我更倾向于接受这种观点)。这个过程就叫作划界(Bracket)。Bracket这个单词是括号的意思,很形象——用括号包住一个范围,就是划界。在某些书中,划界算法也被称为进退法。
建议的一种改进过的黄金搜索算法)可以处理函数非单峰的情况,但是,在没有确定函数在一个区间内是单峰的之前,即使在搜索过程中,函数值持续减小,我们也不能说极小值是一定存在的,因此,找出一个区间,在此区间之内使函数是单峰的,这个过程是必需的(我更倾向于接受这种观点)。这个过程就叫作划界(Bracket)。Bracket这个单词是括号的意思,很形象——用括号包住一个范围,就是划界。在某些书中,划界算法也被称为进退法。
【1】什么是单峰区间?什么是单峰函数?
从字面上理解,“单峰”即函数只有一个峰,如下图所示(在区间[-8,8]内是单峰的):
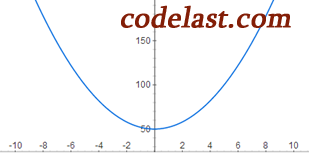
文章来源:http://www.codelast.com/
而下面的这个函数,在区间[2,14]内就不是单峰函数了:
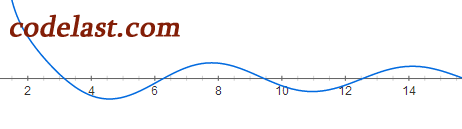
现在,我们再用数学的话来定义一下单峰区间和单峰函数:
![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 为
为  的子集,存在
的子集,存在 ![{\alpha ^*} \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_e48ac27bb5429028836b36729e3bfc66.gif) ,使得
,使得  在
在 ![[a,{\alpha ^*}]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_bfc3057d694a9b06bb46943bf39a0e7b.gif) 上严格单调减,在
上严格单调减,在 ![[{\alpha ^*},b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_ead4fb17a0c4148758ef1619b8d9f56a.gif) 上严格单调增,则称
上严格单调增,则称 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 是
是  的单峰区间,
的单峰区间,  是
是 ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 上的单峰函数。
上的单峰函数。
文章来源:http://www.codelast.com/
【2】“划界”是如何实现的
方法是:寻找使函数值达到“高→低→高”的3个点。
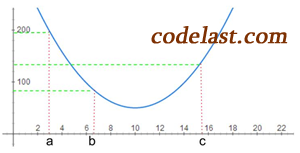
如上图所示,当我们找到  这样3个点的时候,它们就能确定一个单峰区间了。
这样3个点的时候,它们就能确定一个单峰区间了。
一定有人会有疑问说:这不一定,万一  之间还有一个峰怎么办?确实,这里举的例子并不是一个完善的例子,在一个实用的划界程序中,它所做的考虑会非常多,各种意外情况都要处理,此处只是为了说明“划界”是怎么一回事,以及一个最简单的划界程序是怎么做的。
之间还有一个峰怎么办?确实,这里举的例子并不是一个完善的例子,在一个实用的划界程序中,它所做的考虑会非常多,各种意外情况都要处理,此处只是为了说明“划界”是怎么一回事,以及一个最简单的划界程序是怎么做的。
文章来源:http://www.codelast.com/
与各种教科书上仅有令人讨厌的公式说明不同(从不考虑读者的感受),我把几个简单的划界步骤画成了几幅图,我觉得有小学文凭已经足够理解了(一图胜千言):
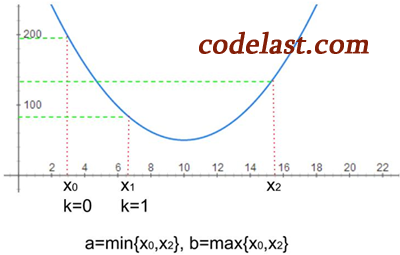
①:
文章来源:http://www.codelast.com/
起始点为  ,假设一开始向右寻找,步长为
,假设一开始向右寻找,步长为  ,图中的
,图中的  表示迭代的次数。
表示迭代的次数。
则第一点挪动到了  ,计算函数值,发现
,计算函数值,发现  ,很好,“高→低→高”的3点中,我们已经有了两点。
,很好,“高→低→高”的3点中,我们已经有了两点。
然后下一点我们挪动到  ,这里用加倍系数
,这里用加倍系数  来乘以步长是为了加速搜索的过程。再计算函数值,发现
来乘以步长是为了加速搜索的过程。再计算函数值,发现  ,很好,我们已经找到了“高→低→高”的3点。任务完成,
,很好,我们已经找到了“高→低→高”的3点。任务完成, ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 即为所求区间。
即为所求区间。
总结一下步骤就是:


文章来源:http://www.codelast.com/
②:
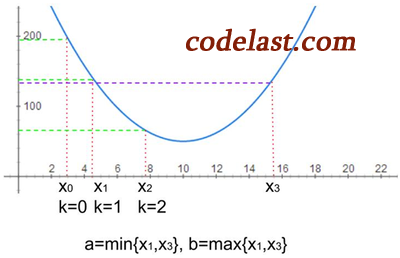
如果运气没那么好,例如:
文章来源:http://www.codelast.com/
即:
和①一样,搜索也经历了  这几个点,与①不同的是,到了
这几个点,与①不同的是,到了  点之后,我们发现其函数值仍然小于
点之后,我们发现其函数值仍然小于  点处的函数值,也就是说,我们还没有找到“高→低→高”的3点。
点处的函数值,也就是说,我们还没有找到“高→低→高”的3点。
于是我们继续放大步长,令  ,再计算函数值,发现
,再计算函数值,发现  ,很好,我们已经找到了“高→低→高”的3点。任务完成,
,很好,我们已经找到了“高→低→高”的3点。任务完成, ![[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_2c3d331bc98b44e71cb2aae9edadca7e.gif) 即为所求区间。
即为所求区间。
总结一下步骤就是:

 (加大步长)
(加大步长)
 (继续加大步长)
(继续加大步长)
文章来源:http://www.codelast.com/
③:
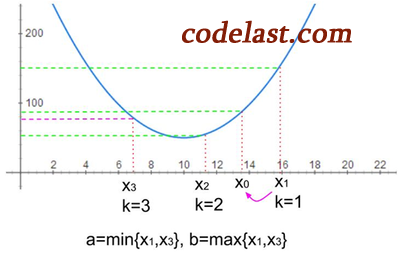
①是向右搜索,如果我们运气更差一些,一开始就是个错误(应该向左搜索),怎么办?
文章来源:http://www.codelast.com/
如上图,起始点为  ,第一个挪动到的点起始点为
,第一个挪动到的点起始点为  ,而
,而  处的函数值竟然比起始点
处的函数值竟然比起始点  处的函数值要大(函数值不降反升)。于是我们可以向左搜索(将步长
处的函数值要大(函数值不降反升)。于是我们可以向左搜索(将步长  设为负值),并且把
设为负值),并且把  挪到
挪到  ,继续按①的节奏进行下去。
,继续按①的节奏进行下去。
总结一下步骤就是:
 (发现函数值不降反升)
(发现函数值不降反升)
 (步长设为负值,向左搜索)
(步长设为负值,向左搜索)
 (重置
(重置  点)
点)

 (加大步长,函数值回升,停止搜索)
(加大步长,函数值回升,停止搜索)
文章来源:http://www.codelast.com/
【3】加快划界的速度:逆抛物内插
有没有什么办法可以加快划界的速度呢?有,逆抛物内插(Inverse Parabolic Interpolation)就是一种技术,它可以使得划界算法超线性收敛。
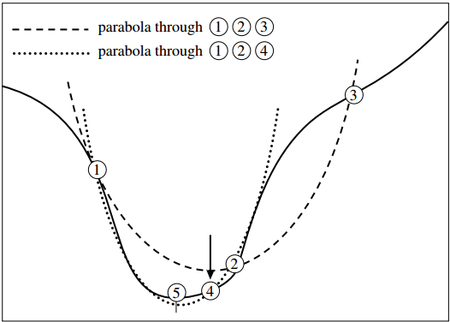
为了解释什么是逆抛物内插,这里用书上的一幅图来讲解:
文章来源:http://www.codelast.com/
如图,实线为目标函数曲线。在该曲线上,如果我们要尽快逼近极小值点,可以这样做:通过①②③三点作一条抛物线(图中粗虚线所示),可以计算出该抛物线的极小值点的横坐标,从而可以找到同一横坐标下,目标函数上的点,即点④;然后再过①②④三点作一条抛物线(图中细虚线所示),可以计算出该抛物线的极小值点的横坐标,从而又可以找到同一横坐标下,目标函数上的点,即点⑤。这样,我们就很快地逼近了极小值。
那么,过三点的抛物线,其极小值点的横坐标怎么求?
已知函数  ,过
,过  三点的抛物线,其极小值点的横坐标
三点的抛物线,其极小值点的横坐标  为:
为:
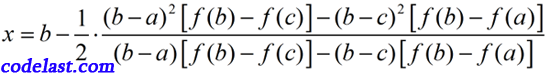
文章来源:http://www.codelast.com/
注:为什么叫“逆”?因为上面的方法是用来求横坐标  ,而不是求
,而不是求  的。
的。
有人会问:划界的目标就是找到3个点,而你怎么会预先知道3个点的坐标,从而进行逆抛物内插?这不是因果倒置了吗?
其实,这里的三个点,并不是划界的结果,而是初始的猜测,通过初始的猜测点进行逆抛物内插,再根据内插点的不同情况,分别作不同的处理,最终可以找到划界的3个点。
例如,我们总要知道两个初始点  吧?好吧,如果你已知的真的只有一个点
吧?好吧,如果你已知的真的只有一个点  ,那么
,那么  就随便取比
就随便取比  大一点的值好了,这也能凑够两个点啊。通过这两个点,可以通过
大一点的值好了,这也能凑够两个点啊。通过这两个点,可以通过  来得到猜测的第一个
来得到猜测的第一个  点(这里的
点(这里的  表示一个系数,例如1.618),从而可以通过这3点开始逆抛物内插。
表示一个系数,例如1.618),从而可以通过这3点开始逆抛物内插。
文章来源:http://www.codelast.com/
一个实用的划界程序还是挺复杂的——这里的复杂是比较于上面陈述的最简单的划界算法来说的,因为要保证程序在很多“意外情况”下都能正确运行,必须做很多工作。这里就不分析具体的程序了,大家可以到网上找来看一下。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

那个逆抛物内插是怎么加快速度找到三个点的呢?
楼主写的一系列优化算法非常通俗,调理分明!前段时间一直访问不了楼主的网站,这几天又能访问了!如果能整理成pdf文档那就更好了!
赞