[原创]使用一维搜索(line search)的算法的收敛性

在最优化领域中，有一类使用一维搜索（line search）的算法，例如牛顿法等。这类算法采用的是 确定搜索方向→进行一维搜索→调整搜索方向→进行一维搜索 的迭代过程来求解。那么，这类算法应该满足什么条件的时候才能收敛？本文将略为讨论一下。请务必看清本文的标题：不是讨论line search的收敛性，而是讨论使用line search的算法的收敛性。

【1】搜索方向条件
搜索方向 ${d_k}$ 满足什么条件时算法才能收敛？谈到这个问题，首先就要定义搜索方向——要有一个“参照物”，要不然何来方向之说呢？
用 ${d_k}$ 与负梯度 $- {g_k}$ 的夹角 ${\theta _k}$ 来衡量搜索方向。我们先给出结论： ${\theta _k}$ 应满足：

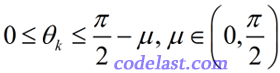
文章来源：http://www.codelast.com/
为了说明这个式子是怎么来的，需要先说明两个向量（ ${d_k}, - {g_k}$ 都是向量）夹角的余弦怎么计算：

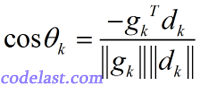
文章来源：http://www.codelast.com/
分子 ${ - {g_k}^T{d_k}}$ 是两个向量的点积（数量积），分母 ${\left\| {{g_k}} \right\|\left\| {{d_k}} \right\|}$ 是两个向量的范数之积，分母>0。
由上面 ${\theta _k}$ 的取值范围可知 $\cos {\theta _k} \in (0,1)$ ，即 $\cos {\theta _k} > 0$ ，因此 ${g_k}^T{d_k} < 0$
所以，根据泰勒展开式（忽略掉高阶无穷小部分）：
$f({x_k} + \alpha {d_k}) = f({x_k}) + \alpha {g_k}^T{d_k} + o(\alpha )$
我们可知， $f({x_k} + \alpha {d_k}) < f({x_k})$ ，即函数值是下降的——下降正是最优化的目标。
所以你现在明白为什么 ${\theta _k}$ 要满足上面的条件了。
文章来源：http://www.codelast.com/
【2】两个关于收敛性的重要理论
这两个理论非常重要，作个比喻，如果你要自己设计一个使用line search技术的算法，并且要保证它能收敛的话，那么，你可能就要让你的算法符合这两个理论的要求。
其中一个理论描述了使用精确line search技术的算法的收敛性，另一个描述了使用不精确line search技术的算法的收敛性。
①适用于使用精确line search技术的算法
设最优化算法产生的点序列为 $\{ {x_k}\} ,\{ f({x_k})\}$ ，对任意 ${x_0} \in {R^n}$ ，目标函数的梯度 $g(x)$ 在水平集 $L = \{ x \in {R^n}:f(x) \le f({x_0})\}$ 上一致连续，若line search的步长 ${\alpha _k}$ 满足精确搜索条件 ${\alpha _k} = \arg \mathop {\min }\limits_{\alpha > 0} f({x_k} + \alpha {d_k})$ ，搜索方向 ${d_k}$ 与 $- {g_k}$ 的夹角满足前面所说的搜索方向条件，那么，必然会发生下面3种情况中的一种：
（1）存在某个有限的 $k$ ，使得 ${g_k} = 0$
（2） $f({x_k}) \to - \infty$
（3） ${g_k} \to 0$
文章来源：http://www.codelast.com/
其中，（3）是最常见的情况，（1）和（2）很少出现——书上是这么说的，至于为什么，我不知道。
（3）中的 ${g_k} \to 0$ 又是个什么概念呢？大家可以想像一下二维平面上的寻优过程，一个图像类似于抛物线的函数，当搜索点逐渐向极小值点逼近时，其梯度 ${g_k}$ 正是趋于0的。

另外，上面出现了“一致连续”的概念，我不太了解，这里摘录Wiki的部分内容：
一致连续性描述定义在一定度量空间上的函数的性质。与连续性刻画函数在局部的性质不同，一致连续刻画的是函数的整体性质。一致连续是比连续更苛刻的条件。一个函数在某度量空间上一致连续，则其在此度量空间上必然连续，但反之未必成立。直观上，一致连续可以理解为，当自变量 $x$ 在足够小的范围内变动时，函数值 $y$ 的变动也会被限制在足够小的范围内。
文章来源：http://www.codelast.com/
②适用于使用不精确line search技术的算法
设最优化算法产生的点序列为 $\{ {x_k}\} ,\{ f({x_k})\}$ ，对任意 ${x_0} \in {R^n}$ ，目标函数的梯度 $g(x)$ 在 ${R^n}$ 上Lipschitz连续，若line search的步长 ${\alpha _k}$ 满足Wolfe-Powell准则，搜索方向 ${d_k}$ 与 $- {g_k}$ 的夹角满足前面所说的搜索方向条件，那么，必然会发生下面3种情况中的一种：