【正文】
总学时:196学时,6学时/周,教学过程1年
内容:一元、多元函数微分学和积分学、矢量代数、空间解析几何、无穷级数和微分方程。
目的:掌握高数基本知识、基本理论、基本计算方法(所谓的“三基”),提高数学素养;培养学生的抽象思维和逻辑推理的能力、辩证的思想方法;培养学生的空间想象能力;培养学生分析问题和解决问题的能力。为学生进一步学习数学打下一定基础,为学习专业的后继课程准备必要的数学基础。
第1章 函数
§1 函数的概念
一、区间、邻域
自然数集 N
整数集 Z
有理数集 Q
实数集 R
文章来源:http://www.codelast.com/
建立数轴后:

建立某一实数集A与数轴上某一区间对应
区间:设有数  ,则称实数集
,则称实数集  为一个开区间,记为
为一个开区间,记为 
即 
a称为  的左端点,b称为
的左端点,b称为  的右端点。
的右端点。

闭区间: ![\left[ {a,b} \right] = \left\{ {x|a \le x \le b} \right\}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_9a96af7d0ed09eb2d80b2d7c945c1e21.gif)
![a \in [a,b],b \in [a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_5195259d395078a9e2261a98ce31ee15.gif)
文章来源:http://www.codelast.com/
半开区间: 
![(a,b] = \{ x|a < x \le b\} ,a \in (a,b],b \notin (a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_11e490eeacb0f9bd245dedc1d8d3dbb3.gif)
a,b都是确定的实数,称 ![(a,b),[a,b),(a,b],[a,b]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_b72da359d48332d591bfb4c0e35ecd7e.gif) 为有限区间,“
为有限区间,“  ”称为区间长度。
”称为区间长度。
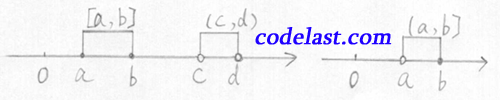
记号:
 ——正无穷大
——正无穷大
 ——负无穷大
——负无穷大
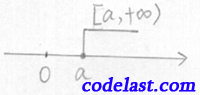
区间:


![( - \infty ,b] = \{ x|x \le b\}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_1d865af894510eee4f37686267ed515a.gif)

称为无穷区间(或无限区间)
文章来源:http://www.codelast.com/
邻域:设有两个实数  ,则称实数集
,则称实数集  为点
为点  的
的  邻域,记为
邻域,记为 

 称为
称为  的中心,
的中心,  称为邻域
称为邻域  的半径。
的半径。
文章来源:http://www.codelast.com/
(第1课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
