【正文】
例2. 重要极限之一： \(\mathop {\lim }\limits_{\alpha \to 0} \frac{{\sin \alpha }}{\alpha } = 1\)
证：
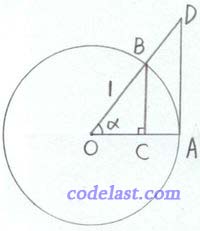
在单位圆内，设圆心角 \(\angle AOB = \alpha ,\;0 < \alpha < \frac{\pi }{2}\)
\(BC = \sin \alpha \)
\(\stackrel \frown {AB} = 1 \cdot \alpha = \alpha \) （弧长 = 半径×圆心角）
\(AD = \tan \alpha \)
\(\bigtriangleup AOB\) 面积 < 圆扇形 \(AOB\) 面积 < \(\bigtriangleup AOD\) 面积
即 \(\frac{1}{2}AO \cdot BC < \frac{1}{2}AO \cdot \stackrel \frown {AB} < \frac{1}{2}AO \cdot AD\)
即 \(BC < \stackrel \frown {AB} < AD\)
\(\sin \alpha < \alpha < \tan \alpha \)
因为 \(0 < \alpha < \frac{\pi }{2},\;\sin \alpha > 0\)
所以上面的不等式同除以 \(\sin \alpha \) 得：
\(1 < \frac{\alpha }{{\sin \alpha }} < \frac{1}{{\cos \alpha }}\)
即 \(1 > \frac{{\sin \alpha }}{\alpha } > \cos \alpha \)
文章来源：http://www.codelast.com/
如果 \( - \frac{\pi }{2} < \alpha < 0\) ，令 \(t = - \alpha \)
\(\cos \alpha = \cos ( - t) = \cos t\)
\(\frac{{\sin \alpha }}{\alpha } = \frac{{\sin ( - t)}}{{ - t}} = \frac{{ - \sin t}}{{ - t}} = \frac{{\sin t}}{t}\)
所以上面的不等式对 \(\alpha > 0\) 和 \(\alpha < 0\) 都正确
因为 \(\mathop {\lim }\limits_{\alpha \to 0} 1 = 1,\;\mathop {\lim }\limits_{\alpha \to 0} \cos \alpha = 1\)
所以根据夹挤准则，得 \(\mathop {\lim }\limits_{\alpha \to 0} \frac{{\sin \alpha }}{\alpha } = 1\)
文章来源：http://www.codelast.com/
例1. 求 \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin \alpha x}}{{\sin \beta x}}\;\;(\alpha \ne 0,\;\beta \ne 0)\) ，其中 \(\alpha ,\beta \) 均为常数。
解：
原式 \( = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\frac{{\sin \alpha x}}{{\alpha x}}}}{{\frac{{\sin \beta x}}{{\beta x}}}} \cdot \frac{{\alpha x}}{{\beta x}}} \right) = \frac{{\mathop {\lim }\limits_{x \to 0} \frac{{\sin \alpha x}}{{\alpha x}}}}{{\mathop {\lim }\limits_{x \to 0} \frac{{\sin \beta x}}{{\beta x}}}} \cdot \frac{\alpha }{\beta } = \frac{1}{1} \cdot \frac{\alpha }{\beta } = \frac{\alpha }{\beta }\)
例2. 求 \( = \mathop {\lim }\limits_{x \to 0} \)
解：
原式 \( = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin 2x}}{{\cos 2x}}}}{x} = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\sin 2x}}{x} \cdot \frac{1}{{\cos 2x}}} \right) = 2\mathop {\lim }\limits_{x \to 0} \frac{{\sin 2x}}{x} \cdot \mathop {\lim }\limits_{x \to 0} \frac{1}{{\cos 2x}} = 2 \cdot 1 \cdot 1 = 2\)
文章来源：http://www.codelast.com/
例3. 求 \(\mathop {\lim }\limits_{x \to 0} \frac{{\tan x - \sin x}}{{{x^3}}}\)
解：
原式 \( = \mathop {\lim }\limits_{x \to 0} \frac{{\frac{{\sin x}}{{\cos x}} - \sin x}}{{{x^3}}} = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\sin x}}{x} \cdot \frac{{1 - \cos x}}{{{x^2}\cos x}}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\frac{{\sin x}}{x} \cdot \frac{{2{{\sin }^2}\frac{x}{2}}}{{{x^2}}} \cdot \frac{1}{{\cos x}}} \right)\)
\( = \mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} \cdot \frac{1}{2}\mathop {\lim }\limits_{x \to 0} {\left( {\frac{{\sin \frac{x}{2}}}{{\frac{x}{2}}}} \right)^2} \cdot \mathop {\lim }\limits_{x \to 0} \frac{1}{{\cos x}} = 1 \cdot \left( {\frac{1}{2} \cdot {1^2}} \right) \cdot 1 = \frac{1}{2}\)
文章来源：http://www.codelast.com/
二、准则2 单调有界准则
如果数列 \(\{ {u_n}\} \) 满足 \({u_1} \le {u_2} \le {u_3} \le \cdots \le {u_n} \le \cdots \) ，则称 \(\{ {u_n}\} \) 为单调增数列。
若其满足 \({u_1} \ge {u_2} \ge {u_3} \ge \cdots \ge {u_n} \ge \cdots \) ，则称 \(\{ {u_n}\} \) 为单调减数列。
极限存在的单调有界准则就是：若单调数列 \(\{ {u_n}\} \) 是有界的，则 \(\mathop {\lim }\limits_{n \to \infty } {u_n}\) 存在。
例1. 重要极限之二： \(\mathop {\lim }\limits_{x \to \infty } {\left( {1 + \frac{1}{x}} \right)^x} = e\)
证：
先证 \(x = n,\;n \in N\) ，即 \(n\) 为正整数的情况。
通项 \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\) ，要证 \(\{ {u_n}\} \) 单调增且有界。
设 \(a > b > 0\) （ \(a,b\) 为实数）
\({a^{n + 1}} - {b^{n + 1}} = (a - b)({a^n} + {a^{n - 1}}b + {a^{n - 2}}{b^2} + \cdots + {b^n})\) （中学因式分解知识）
\( < (a - b)({a^n} + {a^{n - 1}}a + {a^{n - 2}}{a^2} + \cdots + {a^n})\) （把上个式子中的 \(b\) 换成 \(a\) ，由 \(a > b\) 可得此不等式）
\( = (a - b)({a^n} + {a^n} + {a^n} + \cdots + {a^n})\) （共 \(n + 1\) 个 \({a^n}\) ）
\( = (a - b)(n + 1){a^n}\)
\( \Rightarrow {a^n}\left[ {(n + 1)b - na} \right] < {b^{n + 1}}\)
取 \(a = 1 + \frac{1}{n},\;b = 1 + \frac{1}{{n + 1}}\) ，则 \(a,b\) 的取值满足 \(a > b > 0\)
把 \(a = 1 + \frac{1}{n},\;b = 1 + \frac{1}{{n + 1}}\) 代入上面推导出的不等式，得：
\({\left( {1 + \frac{1}{n}} \right)^n}\left[ {\left( {n + 1} \right)\left( {1 + \frac{1}{{n + 1}}} \right) - n\left( {1 + \frac{1}{n}} \right)} \right] < {\left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1}}\)
\( \Rightarrow {\left( {1 + \frac{1}{n}} \right)^n} \cdot 1 < {\left( {1 + \frac{1}{{n + 1}}} \right)^{n + 1}} \Rightarrow {u_n} < {u_{n + 1}}\;(n = 1,2, \cdots )\)
这说明 \({u_n}\) 是单调增数列。
文章来源：http://www.codelast.com/
再设 \(a = 1 + \frac{1}{{2n}},\;b = 1\) ，则 \(a,b\) 的取值满足 \(a > b > 0\) 。代入上面推导出的不等式：
\({\left( {1 + \frac{1}{{2n}}} \right)^n}\left[ {(n + 1) \cdot 1 - n\left( {1 + \frac{1}{{2n}}} \right)} \right] < {1^{n + 1}} \Rightarrow {\left( {1 + \frac{1}{{2n}}} \right)^n} < 2\)
两边都是 \( > 1\) 的数，故两边平方，得：
\({\left( {1 + \frac{1}{{2n}}} \right)^{2n}} < 4\)
即 \({u_{2n}} < 4\)
又由前面已经证明的 \({u_n}\) 是单调增数列，可知：
\({u_{2n - 1}} < {u_{2n}} < 4\)
即 \({u_n} < 4\;(n = 1,2, \cdots )\) ，也即 \({u_n}\) 有界。
文章来源：http://www.codelast.com/
因为 \({u_n}\) 单调增且有界
所以根据准则2， \(\mathop {\lim }\limits_{n \to \infty } {u_n} = \mathop {\lim }\limits_{n \to \infty } {\left( {1 + \frac{1}{n}} \right)^n} = e\)
（注：看到这里，有人可能会有疑问：上面折腾了那么多，无非就是证明了极限是存在的，但是并没有证明这个极限的值是什么啊！你怎么知道它是等于 \(e\) 的呢？没错，这里根本就是“把这个极限值记为 \(e\) ”，而不是知道了这个值具体等于多少，所以不要觉得奇怪）
上面成功地证明了当 \(x\) 为正整数时的情况，下一节课将证明当 \(x\) 是连续自变量时 \(\mathop {\lim }\limits_{x \to \infty } {\left( {1 + \frac{1}{x}} \right)^x} = e\) 也成立。
文章来源：http://www.codelast.com/
（第15课完）
文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处：codelast.com
感谢关注我的微信公众号（微信扫一扫）：
