【正文】
去心邻域:把  的中心点
的中心点  去掉,称为点
去掉,称为点  的去心邻域,记为
的去心邻域,记为 
注:其中,  表示去掉由
表示去掉由  这一个数组成的数集。
这一个数组成的数集。
二、函数概念
例1. 设圆的半径为  ,它的面积
,它的面积  ,当
,当  在
在  内任取一个数值(记为
内任取一个数值(记为  )时,由关系式
)时,由关系式  就可以确定A的对应数值。
就可以确定A的对应数值。
文章来源:http://www.codelast.com/
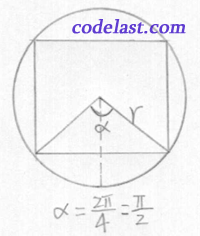
例2. 设有半径为  的圆,作圆的内接正
的圆,作圆的内接正  边形,每一边对应的圆心角
边形,每一边对应的圆心角  ,周长
,周长  ,当边数
,当边数  在自然数集
在自然数集  任取一个数,通过关系式
任取一个数,通过关系式  就有一个
就有一个  对应确定数值。
对应确定数值。
函数定义:设有数集  ,
,  是一个确定的对应法则,对
是一个确定的对应法则,对  ,通过对应法则
,通过对应法则  都有唯一的
都有唯一的  与
与  对应,记为
对应,记为  ,或
,或  ,则称
,则称  为定义在
为定义在  上的函数。
上的函数。
其中  称为
称为  的定义域,常记为
的定义域,常记为  。
。
 ——自变量,
——自变量,  ——因变量。
——因变量。
当  遍取
遍取  中的一切数时,那么与之对应的
中的一切数时,那么与之对应的  值构成一个数集
值构成一个数集  ,称
,称  为函数
为函数  的值域。
的值域。
文章来源:http://www.codelast.com/
注意:
(1)一个函数是由  的对应法则
的对应法则  与
与  的取值范围
的取值范围  所确定的。把“对应法则
所确定的。把“对应法则  ”、“定义域”称为函数定义的两个要素。
”、“定义域”称为函数定义的两个要素。
例如,  这个式子,由于
这个式子,由于  ,而只有当
,而只有当  时,
时,  才有意义,因此这个式子不构成函数关系。
才有意义,因此这个式子不构成函数关系。
又例如,  与
与  不是同一个函数,因为定义域不同。而
不是同一个函数,因为定义域不同。而  与
与  是同一个函数,因为定义域相同。
是同一个函数,因为定义域相同。
(2)函数的值域是定义域和对应法则共同确定的。
(3)确定函数定义域时,注意:若函数有实际意义,需依据实际问题是否有意义来确定。
若函数不表示某实际问题,则定义域为自变量所能取得的使函数  成立的一切实数所组成的数值。
成立的一切实数所组成的数值。
函数的几何意义:设函数  定义域为
定义域为  ,
,  ,对应函数值
,对应函数值  在
在  平面上得到点
平面上得到点  ,当
,当  遍取
遍取  中一切实数时,就得到点集
中一切实数时,就得到点集  。点集
。点集  称为函数
称为函数  的图形。
的图形。
文章来源:http://www.codelast.com/
三、函数的几个简单性质
1. 函数的有界性
若  ,则称
,则称  在区间
在区间  上有界。否则称
上有界。否则称  在
在  上无界。
上无界。
注:  是“使得,满足于”的意思,
是“使得,满足于”的意思,  表示某个区间。
表示某个区间。
例如,  在
在  )上是有界的(因为
)上是有界的(因为  )。
)。
又如,  在
在  上有界。
上有界。
对任何正数  (无论多么大),总
(无论多么大),总  ,则称
,则称  在
在  上无界。
上无界。
例如,  在
在  内无界。
内无界。
证明:
对给定的  (不妨设
(不妨设  ),无论M多么大,必存在
),无论M多么大,必存在  ,使
,使 
文章来源:http://www.codelast.com/
(第2课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
