【正文】
(1)由于自变量  的变化引起函数
的变化引起函数  变化的“快慢”问题——函数的变化率/导数。
变化的“快慢”问题——函数的变化率/导数。
(2)由于自变量的微小改变(增量  很小时)引起
很小时)引起  的改变量
的改变量  的近似值问题——微分问题。
的近似值问题——微分问题。
(3)求导数或微分——微分法。
 1 导数概念
1 导数概念一、两个实例
1.直线运动的瞬时速度问题
设质点沿直线作非匀速运动,其走过的路程  与时间
与时间  的函数关系
的函数关系  ,求某一时刻
,求某一时刻  时的瞬时速度。
时的瞬时速度。
设从时刻  到
到  这段时间内质点走过的路程为
这段时间内质点走过的路程为 

从  到
到  这段时间内,平均速度
这段时间内,平均速度 
对非匀速运动的质点,平均速度  可以作为
可以作为  时刻瞬时速度的近似值(
时刻瞬时速度的近似值(  很小时):
很小时):

 越小,
越小,  与
与  越接近。
越接近。
如果当  时,
时,  的极限存在,即:
的极限存在,即:

则有 
文章来源:http://www.codelast.com/
2.曲线在一点处的切线斜率
切线:当  时,割线
时,割线  的极限位置
的极限位置  称为曲线的切线
称为曲线的切线
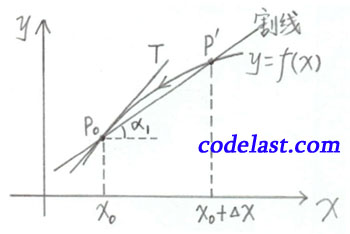
割线: 
割线斜率 
当  时,
时, 

切线  的斜率
的斜率 
(注:  为切线的倾斜角)
为切线的倾斜角)
文章来源:http://www.codelast.com/
二、导数定义
<定义1> 设  在
在  内有定义,当自变量
内有定义,当自变量  在
在  点有增量
点有增量  (
(  ),函数
),函数  相应的增量为
相应的增量为  ,如果极限
,如果极限  存在,则称
存在,则称  在
在  点可导,并称此极限值为
点可导,并称此极限值为  在
在  点的导数。
点的导数。
记为:

即 
文章来源:http://www.codelast.com/
直线运动的瞬时速度 
曲线在  的切线斜率
的切线斜率 
导数定义的另一种极限形式——  在
在  点的导数可以定义为:
点的导数可以定义为:
若记  (即
(即  )
)
当  时,
时, 


文章来源:http://www.codelast.com/
 在
在  点可导,记为
点可导,记为 
 在
在  内每一点处都可导,则称
内每一点处都可导,则称  在
在  内可导,记为
内可导,记为 
 在区间
在区间  上可导,记为
上可导,记为 
若  在
在  内可导,
内可导,  ,就有
,就有  与
与  对应,由函数定义,可知
对应,由函数定义,可知  是定义在
是定义在  上的函数,
上的函数,  称为导函数,一般还称为导数。
称为导函数,一般还称为导数。
文章来源:http://www.codelast.com/
例1. 求函数  的导函数(
的导函数(  )
)
解:
 定义域为
定义域为 
 ,自变量有增量
,自变量有增量  ,且
,且 
函数  对应的增量
对应的增量 
作比值:

求极限:

即 
文章来源:http://www.codelast.com/
(第22课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
