[原创]高等数学笔记(23)

【前言】
请看此文。
要查看高等数学笔记合集，请看这里。

【正文】
<定义2> 设函数 $f(x)$ 在 ${x_0}$ 点的左侧 $[{x_0} + \Delta x,{x_0}]$ （ $\Delta x < 0$ ）有定义，如果极限 $\mathop {\lim }\limits_{\Delta x \to {0^ - }} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}}$ 存在，则称此极限为 $f(x)$ 在 ${x_0}$ 点的左导数，记为 ${{f'}_ - }({x_0}) = \mathop {\lim }\limits_{\Delta x \to {0^ - }} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}}$

类似有右导数：
${{f'}_ + }({x_0}) = \mathop {\lim }\limits_{\Delta x \to {0^ + }} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{\Delta x}}$
显然有：
${f({x_0})}$ 在 ${{x_0}}$ 点可导 $\Leftrightarrow {{f'}_ - }({x_0}),{{f'}_ + }({x_0})$ 存在且 ${{f'}_ - }({x_0}) = {{f'}_ + }({x_0})$
文章来源：http://www.codelast.com/
如果 $f(x)$ 在 $(a,b)$ 内可导，且 ${{f'}_ + }(a)$ 和 ${{f'}_ - }(b)$ 存在，则称 $f(x)$ 在 $[a,b]$ 上可导，记为 $f(x) \in D\left[ {a,b} \right]$

三、导数的几何意义
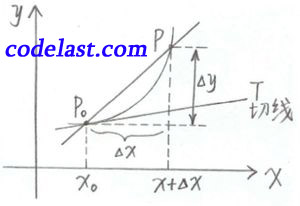
由实例2（曲线上一点处切线的斜率问题）及导数定义：
$f'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}$
可知 $\frac{{\Delta y}}{{\Delta x}}$ 表示割线 ${P_0}P$ 的斜率
$\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = f'({x_0})$

文章来源：http://www.codelast.com/
$f'(x)$ 在几何上表示曲线上一点 ${P_0}({x_0},f({x_0}))$ 点处切线 ${P_0}T$ 的斜率 $f'({x_0}) = \tan \alpha$ ， $\alpha$ 是切线 ${P_0}T$ 的倾角。
根据导数几何意义及平面解析几何关于直线方程的知识（点斜式方程）：
切线方程为： $y - f({x_0}) = f'({x_0})(x - {x_0})$
曲线上点 ${P_0}({x_0},f({x_0}))$ 的法线（过 ${P_0}$ 点且与该点处的切线垂直的直线，称为曲线在 ${P_0}$ 点的法线）方程是什么？
已知：切线斜率 ${k_q} = f'({x_0})$
而切线与法线垂直，故法线斜率 ${k_f} = - \frac{1}{{f'({x_0})}}$ （与切线斜率互为负倒数，其中 $f'({x_0}) \ne 0$ ）
所以法线方程为： $y - f({x_0}) = - \frac{1}{{f'({x_0})}}(x - {x_0})$
若 $y = f(x)$ 在 ${x_0}$ 点处 $f'({x_0}) = \infty$ （表示切线垂直于 $x$ 轴），则切线方程为 $x = {x_0}$
文章来源：http://www.codelast.com/
例1. 求曲线 $y = \frac{1}{{{x^2}}}$ 在 ${P_0}(1,1)$ 处的切线方程和法线方程。
解：先求导数： $y' = - \frac{2}{{{x^3}}}$ ，则 ${\left. {y'} \right|_{x = 1}} = - 2$
切线斜率 ${k_q} = - 2$ ，法线斜率 ${k_f} = \frac{1}{2}$
因此切线方程为： $y - 1 = - 2(x - 1) \Rightarrow 2x + y - 3 = 0$
法线方程为： $y - 1 = \frac{1}{2}(x - 1) \Rightarrow x - 2y + 1 = 0$
文章来源：http://www.codelast.com/
思考：曲线 $y = f({x_0})$ 外有一点 ${M_0}({x_0},{y_0})$ ，过 ${M_0}$ 点作曲线的切线，怎样求该切线的方程？

四、函数的可导性与连续性的关系
<定理> 如果函数 $y = f(x)$ 在 ${x_0}$ 点可导，则 $f({x_0})$ 在 ${x_0}$ 点必定连续。
证：设 $f(x)$ 的自变量 $x$ 在 ${x_0}$ 点有增量 $\Delta x$ ，函数对应的增量 $\Delta y = f({x_0} + \Delta x) - f({x_0})$
要证 $f(x)$ 在 ${x_0}$ 点处连续，也就是要证 $\mathop {\lim }\limits_{\Delta x \to 0} \Delta y = 0$ （注：为什么？见第18课的连续性定义）
由于 $y = f(x)$ 在 ${x_0}$ 点可导，从而有： $\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}$ 存在，且 $\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = f'({x_0})$
根据有极限的函数与无穷小的关系（ $\mathop {\lim }\limits_{x \to {x_0}} f(x) = A \Leftrightarrow f(x) = A + \alpha ,\mathop {\lim }\limits_{x \to {x_0}} \alpha = 0$ ）可知：
$\frac{{\Delta y}}{{\Delta x}} = f'({x_0}) + \alpha$
即： $\Delta y = f'({x_0})\Delta x + \alpha \Delta x$
两边取极限：
$\mathop {\lim }\limits_{\Delta x \to 0} \Delta y = f'({x_0})\mathop {\lim }\limits_{\Delta x \to 0} \Delta x + \mathop {\lim }\limits_{\Delta x \to 0} (\alpha \Delta x)$
（注： $\alpha \Delta x$ 为两个无穷小的乘积，仍为无穷小）
因此函数 $y = f(x)$ 在 ${x_0}$ 点处连续（连续是可导的必要条件）
定理的逆命题不成立，即函数在一点连续，也不一定是可导的。
文章来源：http://www.codelast.com/
（第23课完）

文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤ 
转载需注明出处：codelast.com 
感谢关注我的微信公众号（微信扫一扫）：