【正文】
1. 复合函数
![y = f(u),\;u = \varphi (x)\; \Rightarrow \;y = f[\varphi (x)]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_178b426a123e599c976787abc0cf659d.gif)
注意: ![f[\varphi (x)]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7ff01934bdaba403e9edf06aa667a406.gif) 与
与  定义域不一定相同。
定义域不一定相同。
例1. 设  ,求
,求 ![f[\varphi (x)]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7ff01934bdaba403e9edf06aa667a406.gif) 并确定定义域。
并确定定义域。
解: ![f[\varphi (x)] = \frac{{{{\left[ {\varphi (x)} \right]}^2} + 1}}{{{{\left[ {\varphi (x)} \right]}^2} - 1}} = \frac{{{{\left[ {\frac{1}{{1 + x}}} \right]}^2} + 1}}{{{{\left[ {\frac{1}{{1 + x}}} \right]}^2} - 1}} = - \frac{{{x^2} + 2x + 2}}{{x(x + 2)}}](https://www.codelast.com/wp-content/plugins/latex/cache/tex_05060f524bd264cc7041b29a496523cd.gif)
当  (由
(由  可知)且
可知)且  时
时 ![f[\varphi (x)]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7ff01934bdaba403e9edf06aa667a406.gif) 有定义。即
有定义。即 ![f[\varphi (x)]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_7ff01934bdaba403e9edf06aa667a406.gif) 定义域为:
定义域为:

2. 反函数
设有函数  ,定义域
,定义域  ,值域
,值域  。
。  ,至少可以确定一个
,至少可以确定一个  ,如果把
,如果把  看作自变量,把
看作自变量,把  看作因变量,由函数概念,可以看到一个新函数,记为
看作因变量,由函数概念,可以看到一个新函数,记为  ,称为
,称为  的反函数。
的反函数。
反函数的定义域为  ,值域为
,值域为  ,把
,把  称为直接函数,
称为直接函数,  称为反函数。
称为反函数。
注意:
1. 虽然直接函数  是单值的,但反函数
是单值的,但反函数  不一定是单值的。
不一定是单值的。
例如,函数 ![y = {x^2},\;\;{D_f}:( - \infty , + \infty ),\;\;{V_f}:[0, + \infty ]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_f8643c9451cff8fff3870c2164d5c14c.gif)
反函数  不是单值的(因为对
不是单值的(因为对 ![\forall y \in [0, + \infty ]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_77f68e2ee8759dd0bad2ed808a35f534.gif) ,得到
,得到  ,有两个值
,有两个值  ,为双值函数)。
,为双值函数)。
 是一个单值支。
是一个单值支。
2. 如果直接函数  严格单调,则其反函数
严格单调,则其反函数  也是单值单调的。
也是单值单调的。
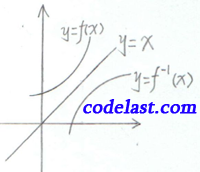
3. 直接函数  与反函数
与反函数  图形相同,习惯上以
图形相同,习惯上以  表示自变量,
表示自变量,  表示因变量,反函数记为
表示因变量,反函数记为  。这时,
。这时,  与
与  的图形关于直线
的图形关于直线  对称,如下图所示:
对称,如下图所示:
例1. 设  ,求反函数
,求反函数 
解:当  时,
时,  ,定义域
,定义域 
当  时,
时,  (因为
(因为  是正数),定义域
是正数),定义域 
综上所述,反函数为:
 初等函数
初等函数6类函数:幂函数、指数函数、对数函数、三角函数、反三角函数、常量函数(例如
 )称为基本初等函数。
)称为基本初等函数。
二、初等函数
由基本初等函数经过有限次的四则运算和有限次的复合步骤所构成的、能够用一个数学式子表达的函数称为初等函数。
例如: 
文章来源:http://www.codelast.com/
初等函数结构分析
例如:分析  的结构
的结构
解:

令 
因此 
文章来源:http://www.codelast.com/
(第4课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):


