【正文】

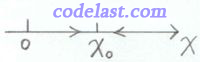
 可以从
可以从  的左侧趋于
的左侧趋于  ,也可以从右侧趋于
,也可以从右侧趋于  。
。
当从  的左侧趋于
的左侧趋于  时,记为
时,记为  ,或
,或 
左极限:对于任意  ,都存在
,都存在  ,凡适合
,凡适合  的一切
的一切  ,对应的函数值
,对应的函数值  都满足
都满足  ,则称
,则称  为
为  的左极限。记为:
的左极限。记为:
 或
或 
可统一表示为 
文章来源:http://www.codelast.com/
右极限:把定义中  改为
改为  ,其他不变,则得到右极限的定义。记为:
,其他不变,则得到右极限的定义。记为:
 或
或 
可统一表示为 
 都存在且极限值都等于
都存在且极限值都等于 
(注:  表示充分必要条件)
表示充分必要条件)
文章来源:http://www.codelast.com/
二、自变量  趋向于无穷大(记为
趋向于无穷大(记为  )时函数
)时函数  的极限
的极限
数列  ,当
,当  时的极限,可以看作是
时的极限,可以看作是  当
当  时的极限的特殊情形。
时的极限的特殊情形。
依照数列极限定义,给出  当
当  时的极限定义:
时的极限定义:
设函数  在
在  充分大时有定义,
充分大时有定义,  为常数,如果对于任意给定的
为常数,如果对于任意给定的  ,都存在正数
,都存在正数  ,使得凡是适合
,使得凡是适合  的一切
的一切  ,对应的函数值
,对应的函数值  都满足
都满足  ,则称当
,则称当  时,
时,  以
以  为极限。记为:
为极限。记为:
 或
或 
如果只考虑  ,且
,且  无限增大(记为
无限增大(记为  ),上面定义中把
),上面定义中把  改为
改为  ,就得到
,就得到  的定义。
的定义。
如果只考虑  ,且
,且  无限增大(记为
无限增大(记为  ),上面定义中把
),上面定义中把  改为
改为  ,就得到
,就得到  的定义。
的定义。
 和
和  都存在且等于
都存在且等于 
(注:  表示充分必要条件)
表示充分必要条件)
文章来源:http://www.codelast.com/
例:证明 
证:


对任意给定的  ,为了使
,为了使  ,只需
,只需  ,即
,即 
因此,对任意给定的  ,取
,取  ,凡是适合不等式
,凡是适合不等式  的一切
的一切  ,对应的函数值
,对应的函数值  都满足:
都满足:

按定义,有 
文章来源:http://www.codelast.com/
三、无穷小量与无穷大量
1. 无穷小(量)
如果  (或
(或  ),则称当
),则称当  (或
(或  )时,
)时,  是无穷小(量)。
是无穷小(量)。
注意:
①不能把一个很小的数看作无穷小。
②常数0可以看作是无穷小的唯一一个常数。
2. 无穷大(量)
如果当  (或
(或  )时,对应的函数值
)时,对应的函数值  的绝对值无限增大,则称当
的绝对值无限增大,则称当  (或
(或  )时,
)时,  是无穷大(量)。
是无穷大(量)。
文章来源:http://www.codelast.com/
或者这样表述:
若对于任意给定的正数  (无论
(无论  多么大),总存在
多么大),总存在  ,凡是适合不等式
,凡是适合不等式  的一切
的一切  ,对应的函数值
,对应的函数值  都满足
都满足  ,则称当
,则称当  时,
时,  是无穷大,记为
是无穷大,记为 
注意:上式并不说明极限存在,只是说明其极限为无穷大量,无穷大不是一个常数。
把上面定义中的“总存在  ,凡是适合不等式
,凡是适合不等式  的一切
的一切  ”改为“总存在正数
”改为“总存在正数  ,凡是适合不等式
,凡是适合不等式  的一切
的一切  ”,其余表述不变,则得到
”,其余表述不变,则得到 
文章来源:http://www.codelast.com/
(第9课完)
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
