[原创]黄金比例搜索算法（Golden Section Search）的实现

黄金比例搜索算法/黄金分割法/0.618法/Golden Section Search/Golden Ratio Search 表达的都是同一个东西，它是一种精确的一维搜索（line search）算法。

黄金比例搜索算法只需要计算目标函数值，而无需计算导数之类的值，因此用起来非常容易，应用广泛。
这里要瞎扯一下：我们都知道黄金比例是0.618，但是你可能没注意到黄金比例还有一些神奇的特性，例如1÷0.618=1+0.618。在建筑学中，也经常使用黄金比例来达到美学效果，例如，代表了全希腊建筑艺术的最高水平的帕特农神庙的立面高与宽的比例为19比31，接近黄金比例。

要使用黄金比例搜索算法，函数 $f(x)$ 需要在某一区间内满足单峰（unimodal）条件。那么什么是单峰呢？看这里。

文章来源：http://www.codelast.com/

在这种情况下，就具备使用该算法的条件了。

有人说，我想用golden section search，但是我怎么能保证在我的搜索区间之内函数是单峰的呢？这就涉及到另一种技术了——划界。试想一下，类似于f(x)=sinx这样的函数图形，在一个区间之内可能有多个波峰波谷，你如何能确定它在一个区间内的极值呢？靠的就是划界。但是，这不在本文的讨论范围内，我们假设你的搜索区间已经使得目标函数在其上是单峰的了。

怎么那么麻烦呢？每次只要一涉及到一个算法，就会用到另一个算法/技术，没办法，数学就是这样层层相套。像最优化中的“单纯形法”那样对其他算法依赖很少的算法，应该算比较少的吧（相比之下，Powell算法真是个麻烦的角色）。

若已知f(x)在[a,b]上单峰，则可用一个含有f(x)最小值的子区间来代替区间I。有一个方法是：选取两个内点c,d（其中c<d），即有a<c<d<b。f(x)的单峰保证了f(c) < max {f(a), f(b)} 且 f(d) < max {f(a), f(b)}。

 

这里又提到了另一个概念：内点。什么是内点呢？

<定义>数学上，集合 S 的内部（又称开核）含有所有直观上“不在 S 的边界上”的 S 的点。S 的内部中的点称为 S 的内点。

文章来源：http://www.codelast.com/

现在有两种情况需要考虑：

（1） $f(c) \le f(d)$ ，则极小值出现在子区间 $[a,d]$ 中，所以我们用d代替b，继续在子区间 $[a,d]$ 中搜索；

（2） $f(d) < f(c)$ ，则极小值出现在子区间 $[c,b]$ 中，所以我们用c代替a，继续在子区间 $[a,c]$ 中搜索。

这里要注意了：我们选取的两个内点不是随意选定的，而是特殊选定的，我们人为地使[a, c]与[d, b]对称，即b-d = c-a，从而：

（3）c=a+(1-r)(b-a)=ra+(1-r)b

（4）d=b-(1-r)(b-a)=(1-r)a+rb

此处r∈(0.5, 1)可以保证c < d

其中，r是未知的，我们要求出来。

我们想让r值在每一个子区间内均保持不变，另外，在每一次搜索的过程中，其中一个旧的内点将被用作新的子区间的一个内点，而一个旧的内点则会成为新的子区间的一个端点。这样，每一次迭代过程中只需要找到一个新点，并且只需要计算一次新函数值。如果f(c) <= f(d)且只需计算一次新函数值的话，那么我们就有：

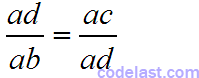
也可以写成：

文章来源：http://www.codelast.com/

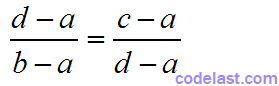
将（3）、（4）式代入此式，得：

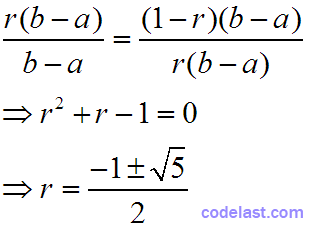
由于r∈(0.5, 1)，故：

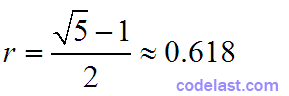
此r值即所谓的黄金比例。平常我们老是说“黄金分割点”，就是这个0.618了。

同理，当 $f(d) < f(c)$ 时，也可求得同样的 $r$ 值。

文章来源：http://www.codelast.com/
下面我用一幅图，从另一个角度来说明黄金比例搜索算法的寻优过程。

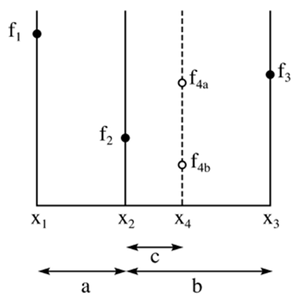
上图来自Wiki。
${x_1},{x_2},{x_3}$ 是已知的三个点（函数值“高→低→高”），它们划界了一个单峰区间，函数值分别为 ${f_1},{f_2},{f_3}$ 。现在的问题是：如何通过一个新点 ${x_4}$ ，不断缩小该区间的范围，从而逼近极小值点？

首先，在最大的区间 $({x_2},{x_3})$ 内安插 ${x_4}$ 是最高效的，因为我们更倾向于相信极小值更有可能出现在大的区间内。
当 ${x_4}$ 的函数值为图中 ${f_{4a}}$ 所示时（即 ${f_{4a}} > {f_2}$ ），此时，区间缩小为 ${x_1},{x_2},{x_4}$ （函数值“高→低→高”的3个点）；当 ${x_4}$ 的函数值为图中 ${f_{4b}}$ 所示时（即 ${f_{4b}} < {f_2}$ ），此时，区间缩小为 ${x_2},{x_4},{x_3}$ （函数值“高→低→高”的3个点），每次迭代均按此规则进行选取。
文章来源：http://www.codelast.com/
其次， ${x_4}$ 应该放在什么位置上呢？随意放置的话，若运气不好，有可能会导致收敛很慢。而事实证明，黄金比例是极好的，即 $\frac{c}{b} = 1 - 0.618$ 。
黄金比例搜索算法是线性收敛的，那么其收敛准则是什么呢？也就是说，我们逐步逼近了极小值所在的区间，到什么程度的时候，我们就可以“收手”，不用再搜索下去了呢？各种参考资料上给出了不同的收敛准则，例如：
$|{x_3} - {x_1}| < \tau \cdot |{x_2}| + |{x_4}|$
或：
$|{x_3} - {x_1}| < \tau \cdot INIT$ （ $INIT$ 为初始区间长度）
文章来源：http://www.codelast.com/
需要一提的是，在给定一个精度 $\delta$ 的情况下，我们可以计算出试验的次数（即需要多少次能找到极小值点）为：
$n \ge \frac{{\lg \delta }}{{\lg 0.618}} + 1$ 取整数。
例如：求函数 $f(x) = x2 - x + 2$ 在 $[ - 1,3]$ 上的极小值点，精度要求 $\delta = 0.08$ （即搜索区间缩小为初始区间长的8%时停止搜索，就认为找到了极小值）。
则：估计试验次数 $n \ge \frac{{\lg 0.08}}{{\lg 0.618}} + 1 = 6.24$ ，实际实验次数 $n = 7$ （按第二个收敛准则）。
文章来源：http://www.codelast.com/
最后来看一下简单的黄金比例搜索算法代码（我根据Wiki中的代码修改的，更易于理解）：

  public static double PHI = (1 + Math.sqrt(5)) / 2;    // 0.618...
  public static double RESPHI = 2 - PHI;  // 0.382...

  /**
   * Golden section search.
   *
   * @author Darran Zhang @ codelast.com
   * @param x1  The left bound of current bounds.
   * @param x2  An interior point between (x1, x3).
   * @param x3  The right bound of current bounds.
   * @param tau The error tolerance to judge the convergence, recommended value is e^0.5, where e is is the required absolute precision of f(x).
   */
  public double goldenSectionSearch(double x1, double x2, double x3, double tau) {
    double x4;
    if (x3 - x2 > x2 - x1) {    // b > a，右半区间长度较大
      x4 = x2 + RESPHI * (x3 - x2);   // x4安插在右半区间
    } else {    // b <= a，左半区间长度较大
      x4 = x2 - RESPHI * (x2 - x1);   // x4安插在左半区间
    }
    if (Math.abs(x3 - x1) < tau * (Math.abs(x2) + Math.abs(x4))) {    // 判断是否达到收敛条件
      return (x3 + x1) / 2;   // 达到收敛条件，取区间长度的一半作为极小值点输出
    }

    assert (function.func(x4) != function.func(x2));

    /* 未达到收敛条件，继续搜索 */
    if (function.func(x4) < function.func(x2)) {    // x4点的函数值如图中f4b所示时
      if (x3 - x2 > x2 - x1) {    // b > a，右半区间长度较大
        return goldenSectionSearch(x2, x4, x3, tau);  // 以x2，x4，x3作为新三点，继续搜索
      } else {    // b <= a，左半区间长度较大
        return goldenSectionSearch(x1, x4, x2, tau);  // 以x1，x4，x2作为新三点，继续搜索
      }
    } else {    // x4点的函数值如图中f4a所示时
      if (x3 - x2 > x2 - x1) {    // b > a，右半区间长度较大
        return goldenSectionSearch(x1, x2, x4, tau);  // 以x1，x2，x4作为新三点，继续搜索
      } else {  // b <= a，左半区间长度较大
        return goldenSectionSearch(x4, x2, x3, tau);  // 以x4，x2，x3作为新三点，继续搜索
      }
    }
  }

这段使用递归方式（并不好）实现的代码要配合上面的图来看。
文章来源：https://www.codelast.com/
➤➤ 版权声明 ➤➤ 
转载需注明出处：codelast.com 
感谢关注我的微信公众号（微信扫一扫）：