对精确的line search(线搜索),有一个重要的定理:
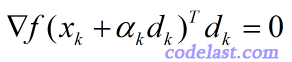
这个定理表明,当前点在  方向上移动到的那一点(
方向上移动到的那一点(  )处的梯度,与当前点的搜索方向
)处的梯度,与当前点的搜索方向  的点积为零。
的点积为零。
其中,  是称之为“步长”的一个实数,它是通过line search算法求出来的。
是称之为“步长”的一个实数,它是通过line search算法求出来的。
为什么会有这样的结论?我们来看看。
对每一个line search过程来说,搜索方向  已经已经是确定的了(在最优化算法中,如何找出一个合适的
已经已经是确定的了(在最优化算法中,如何找出一个合适的  不是line search干的事情)。所以,在一个确定的
不是line search干的事情)。所以,在一个确定的  上,要找到一个合适的
上,要找到一个合适的  ,使得
,使得  这个函数满足
这个函数满足  ,这就是line search的目的。说白了,就是要找到
,这就是line search的目的。说白了,就是要找到  使
使  的函数函数值变小。
的函数函数值变小。
文章来源:http://www.codelast.com/
但是,要小到什么程度呢?假设小到有可能的“最小”,即:

那么,我们称这样的line search为“精确的line search”——你看,这名字好贴切:我们精确地找到了函数值最小的那个点。
既然  是函数值最小的那个点,那么,在该点处的一阶导数(即梯度)为零,所以我们对上式求导(
是函数值最小的那个点,那么,在该点处的一阶导数(即梯度)为零,所以我们对上式求导(  是自变量,
是自变量,  和
和  为常量):
为常量):
![\phi '({\alpha _k}) = {\left[ {f({x_k} + {\alpha _k}{d_k})} \right]^\prime } \cdot (0 + 1 \cdot {d_k}) = {\left[ {f({x_k} + {\alpha _k}{d_k})} \right]^\prime }{d_k} = \nabla f{({x_k} + {\alpha _k}{d_k})^T}{d_k} = 0](https://www.codelast.com/wp-content/plugins/latex/cache/tex_8fb51f475ef3cf5596f7e8252a03b01b.gif)
文章来源:http://www.codelast.com/
这就是我们前面说的定理了。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
