[原创] 蒙特卡罗方法的实例2：计算定积分

查看本系列文章合集，请点击这里。

为了对蒙特卡罗方法有一个直观的印象，本文再举一个实例（计算定积分），以说明蒙特卡罗方法的用途。

什么是定积分

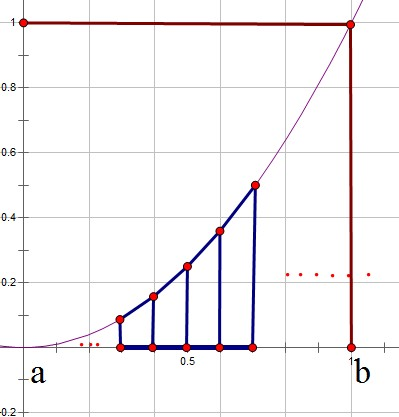
对于一个给定的正实值函数 $f(x)$ ，它在一个实数区间 [a,b]上的定积分 $\int_a^b {f(x)dx}$ 可以理解为在 OXY 坐标平面上，由曲线 (x,f(x))、直线 x=a,x=b以及x轴围成的曲边梯形的面积值。

非蒙特卡罗方法

其中一个计算定积分的方法就是用上面定积分的定义来求它：把面积均分成N个小矩形/梯形，求矩形/梯形面积之和。至于要分到多细才能良好地逼近定积分的真实值，我就不知道是否有什么理论上的说法了。

蒙特卡罗方法

用蒙特卡罗方法来计算定积分，又分成好几种方法——毕竟，蒙特卡罗方法是一类方法的统称，而不是指一种特定的方法。其中一种求定积分的蒙特卡罗方法，可以称之为。和之前的文章中计算圆周率的做法类似，我们这里也用一个实际的函数 $y = {x^2}$ 来说明问题：

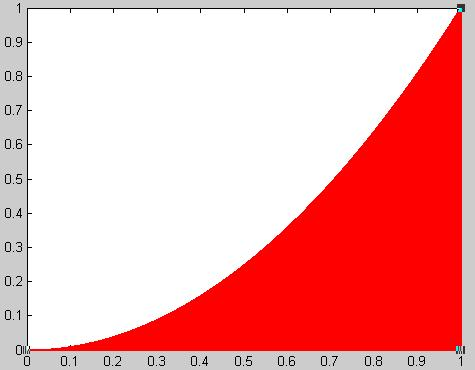
文章来源：https://www.codelast.com/
假设要计算函数在在[0, 1]区间的积分，也就是求红色部分的面积。
然后，在1x1的正方形里生成大量随机点（m个），计算出在红色区域内的点的个数n——判断条件： $y < {x^2}$
最后，n/m 即为红色部分的面积，也就是所求的积分值。
投点法只是其中一种计算定积分的蒙特卡罗方法，当然也是一种很简单的蒙特卡罗方法，另外还有更麻烦的平均值法求定积分——可以利用特殊的采样技巧来提高计算效率，在后面的文章中会讲到。
在后面的文章中，还会解释采样和蒙特卡罗方法有什么关系，先不要急。