在做数据建模或者曲线拟合的时候,我们通常会用到最小二乘法。
假设作为数学模型的函数为  ,其中
,其中  为参数集向量(即一系列的参数),
为参数集向量(即一系列的参数),  为自变量。在这种情况下,为了求出
为自变量。在这种情况下,为了求出  ,需要对下式进行极小化:
,需要对下式进行极小化:
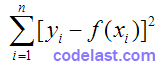
即:对已知的一个数据集  ,能极小化该式的
,能极小化该式的  就是最优参数。但是这个式子是怎么来的呢?
就是最优参数。但是这个式子是怎么来的呢?
它是从最大似然估计方法得到的:对参数  ,能使已知数据集发生的概率越大,那么就说明我们取的
,能使已知数据集发生的概率越大,那么就说明我们取的  越优良。注意,对于一组已知的数据集,参数
越优良。注意,对于一组已知的数据集,参数  几乎不可能使每个
几乎不可能使每个  都满足我们假设的数学模型,因此这里所说的“使已知数据集发生的概率越大”,这个“发生”,是指
都满足我们假设的数学模型,因此这里所说的“使已知数据集发生的概率越大”,这个“发生”,是指 ![{y_i} \in \left[ {f({x_i},S) - \delta ,f({x_i},S) + \delta } \right]](https://www.codelast.com/wp-content/plugins/latex/cache/tex_f5e5b34808d5b625dd297c372e58c58e.gif) ,其中δ为允许的误差。
,其中δ为允许的误差。
假设所有数据点的测量误差独立、符合正态分布,且标准差相等,则每一个数据点发生的概率为:
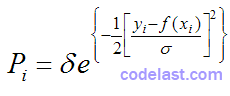
整个数据集同时发生的概率为各数据点概率之积:
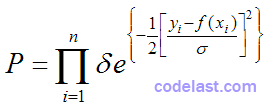
如前文所述:对参数  ,能使已知数据集发生的概率越大,那么就说明我们取的
,能使已知数据集发生的概率越大,那么就说明我们取的  越优良。因此,使上式最大化就是我们的目标。由于
越优良。因此,使上式最大化就是我们的目标。由于  为正常数,
为正常数,  为单调递增函数,因此,想要:
为单调递增函数,因此,想要:
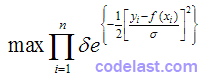
就等于:
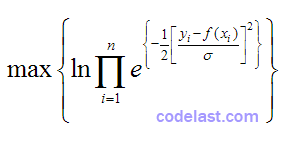
等同于:
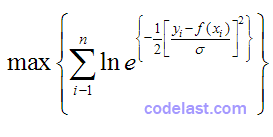
继续化简:
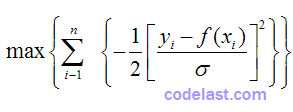
相当于:
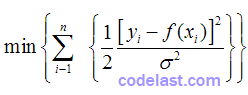
现在,由于  是常数,上式就等同于:
是常数,上式就等同于:
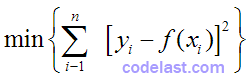
这就得到了我们要推导的结论。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):

NULL
其实从线性代数的角度去理解,会更直接和容易。