以下是我曾在学习“最优化”理论与实践中遇到的一些概念,我刚开始学的时候,有些东西看了很多遍都还觉得很别扭、晦涩难懂,在比较清楚地理解了之后,我打算把它们写下来,并试图以很通俗、但可能不十分严谨的方式解释、呈现出来,以使一部分正在这些概念中挣扎的人能有所解脱。
但是,请注意:有一些是我个人的理解,因个人水平有限,我不能保证完全正确,请您自己辨别。
(1)什么是“搜索方向”
在最优化领域,我们经常会遇到“在某个方向上进行搜索”的说法,例如,使用共轭方向法来寻找最优解的过程中,我们会在共轭方向上进行搜索,那么,这个“方向”到底指的是什么呢?
对一维空间中的方向,我们可能有一种模糊的概念:就像是面前有一条笔直的路,我们沿着它走下去,想要寻找梦中的那个美丽佳人,但是我们不知道她在哪里,于是只能一边走,一边看,有时步子迈大点,有时步子迈小点。这就是一个“在一维方向上进行搜索”的例子。
然后推广到二维平面上:我们可以先在水平方向上移动一段距离,再在垂直方向上移动一段距离,综合起来看,你就可以在在二维平面上移动到任意的地方了。单独看水平或者垂直方向上你的移动,那就是在一个“方向”上的搜索。
同理我们又可以推广到三维空间中。
好吧,现在到了提出一个广泛而又通用的概念的时候了。假设有一个数学函数:
![]()
其自变量为 n 维的,即:
![]()
我们已知了X的初始点X0,现在还有一个实数a,以及一个搜索方向 d (取direction之意),那么,什么才算是在方向 d 上对目标函数的搜索呢?其实就是求函数值:
![]()
并且判断该函数值是否满足一定的条件(例如,不断地减小),如果不满足,就调整搜索方向,并再次计算、并判断的过程。
有了这个概念,我们就可以在N维空间中,沿某一个方向作搜索(尽管我们在几何上想像不出来>三维的空间是什么样子的,但是这并不影响我们定义它)。
举一个简单的例子,就以三维空间为例,假设目标函数为:
![]()
自变量为3维的,假设初始点为X=(2, 4, 3)T,实数 a = 0.5,搜索方向 d=(0, 1, 0)T 。现在,我要在这个方向上移动了:走第一步的时候,移动到了这个点上:
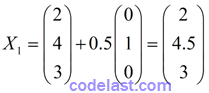
现在计算X1点处的函数值:f(X1)=3×2+4.5+8×3=34.5
另外我们已知了f(X0)=3×2+4+8×3=34
可见f(X1) - f(X0) = 0.5,函数值在方向 d 上移动了一定的距离(这个距离就称之为位移)之后,函数值是增大的。假设我们的要求是函数值减小,则在这个方向上,以步长 a = 0.5 移动时,是无法满足我们的需求的。因此,我们可以调整搜索方向为 d=(0, -1, 0)T ,这样就能实现“函数值不断减小”的需求了。
将上面的简单道理映射到C++程序上:自变量是n维的(即:自变量是一个向量),我们可以用一个std::vector<double>来表示,用于计算目标函数的函数值的C++函数就类似于:
double func(std::vector<double> &vecX)
{
return 3*vecX[0] + vecX[1] + 8*vecX[2];
}
搜索方向的向量 d 也可以用 std::vector<double> 来表示:
std::vector<double> vec_d;
在搜索方向上的移动,用C++代码来描述就是:
std::vector<double> vecX1(3);
for (int i = 0; i < 3; i++)
{
vecX1[i] = vecX0[i] + a * vec_d[i];
}
其中,vecX0 是代表初始点的向量,vecX1 是移动到的点。
然后再判断这一次搜索是否满足要求:
if ( func(vecX1) < func(vecX0) )
{
// 满足要求,作后续处理
}
如上就是“在某个方向上进行搜索”的白话文解释以及相应的示例代码,看起来应该还是挺清晰的吧?
(2)Hesse矩阵/海塞矩阵/黑塞矩阵 是什么?有什么用?
Hesse矩阵,在一些书中音译为海塞矩阵/黑塞矩阵,就是一个函数 f 在一个点 x 处的二阶导数矩阵,通常记为:

矩阵中的每一个分量均为一个函数,并且:由于"二阶混合偏导数在连续的条件下与求导的次序无关",即:

所以,在“连续”条件下,Hesse矩阵是一个对称矩阵。
这个东西与“最优化”有千丝万缕的联系。所以,你必须要知道它的存在。
(3)一维搜索/线搜索,单峰区间,划界,进退法及黄金分割法
一维搜索,又可以叫线搜索,针对的是单峰区间或单峰函数,用于寻找函数在某一区间之内的极值点。
所谓单峰,顾名思义,你可以在头脑中形成这样一种情景:函数的图形画出来就像一个山峰一样,并且只有一个峰。
但是显然,很多函数并不是单峰的。尽管如此,只要我们确定这个函数在某一区间内是单峰的,那么我们仍然可以使用一维搜索技术来寻找极值点。
进退法,其实就是“划界”,顾名思义,就是为函数划定一个边界,在这个边界(定义域)内,函数是单峰的。
为什么要“划界”?因为,如果我们无法保证函数在区间内是单峰的,就无法使用诸如黄金分割法之类的方法来搜索极值。
黄金分割法,又可以叫0.618法(因为我们知道黄金分割比例是0.618),它可以找到一个数学函数在一个单峰区间内的极值点,它与“进退法”(划界)从根本上来说,是不同用途的两种方法——“划界”是黄金分割法的基础,除非你已经确定了一个区间是单峰的,否则,你就要先用划界的方法来确定一个单峰区间,然后再用黄金分割法在单峰区间内来寻找极值。
打个比喻来说:在你的前方,100、200、300米处,分别有3座山,假设我限定了你在200米之内,找到一个最高的点,那么你就可以只爬第一座山,到了山顶之后,就找到了最高点;但是如果我让你在300米之内找到一个最高的点,那么你就需要爬完第一座山,下了山之后继续爬第二座山,然后并且对比两座山的山顶的高度,才知道哪个是最高点。“划界”就像是在这个比喻中我指定的距离,爬山的过程就像是黄金分割法找最高点的过程。显而易见,如果没有“划界”,黄金分割法是没有基础的,这个道理应该不难理解。
(4)袁亚湘是男的
我无意冒犯袁亚湘教授,相反,我非常崇拜他。我写这个标题的原因是,我当初第一次看到这个名字的时候,确实以为是位女教授。袁亚湘教授是最优化领域的著名专家(其导师是更令世人仰视的最优化专家M.J.D Powell),他在依赖域算法方面的研究令人瞩目。2008年我因为做一个软件的原因,到图书馆里去查阅资料,无意中看到了袁亚湘教授写的一本书,当时我第一反应就是:这个女教授写的书好强。由于我既不是数学专业毕业的,也不是计算机专业的(计算机专业的一个研究方向——机器学习领域的算法大多数都是直接或间接地使用了最优化算法),所以恕我知识浅溥,当时都不知袁教授的大名。后来才知道,袁亚湘教授是男的……
这个子项/条目跟最优化概念无关,我只是想记下心中的这一段趣事。这不,您要学习最优化,至少也得听说过袁亚湘吧。
(5)什么是不精确的一维搜索/线搜索
从字面意思就可以想像出来:在一维搜索过程中,如果最后求得的一维变量值可以使得目标函数在某个搜索方向上达到精确的极小值,那么这个搜索过程(搜索方法)就可以称为精确的一维搜索/线搜索;反之,如果达不精确的极小值,而只是使目标函数符合了一个的条件(例如,目标函数值下降了多少),那么就称为不精确的一维搜索/线搜索。
(6)什么是Armijo-Goldstein准则
上文已经说了,在不精确的一维搜索的过程中,目标函数要符合一定的条件,而Armijo-Goldstein准则就是使目标函数满足条件所应遵循的原则——遵循原则,才能保证事情办得成功。
现在,我们来看看Armijo-Goldstein准则的两个表达式:
![]()
![]()
首先是表达式中的若干变量:
![]() :目标函数。f(xk) 表示求 xk 这一点的函数值。
:目标函数。f(xk) 表示求 xk 这一点的函数值。
αk :一个实数,在这里,它有一个名字:步长。这个变量也就是我们在不精确线搜索过程中,需要求的值,换句话说,最后求得的这个值可以使目标函数满足规定的条件。
ρ :一个实数,其取值范围是(0, 0.5)。
gk :目标函数在 xk 这一点的梯度,是一个向量。
dk :搜索方向,是一个向量。
具体解释请看这里。
(7)最优化算法可以用来求“极大值问题”吗
可以。最优化算法是求min f(X),你令 f'(X) = -f(X),就可以把求极大值的问题变为求极小值了。虽然这个问题让人觉得“这不是废话么”,但是我觉得还是会有人当初第一次想到它的时候,心里琢磨着该怎么做吧。这就是答案。
(8)什么是等值线/等高线
在最优化的书和文章中,经常会谈到等值线/等高线,并且作一个图来说明问题,例如这个链接中的图。初学者通常难以理解:这种图是干什么的?为什么它能用来表示搜索的过程?其实,那些图中一个个类似于树的年轮的圈,是人们把三维空间中的立体投影到二维平面上绘制出来的。你可以想像一下,在一片高低不平错落有致的山区中,把这一片山的形状想像成三维空间中的立体,把它们投影到地面上,并且把具有同一海拔的山的切断面绘制出来(就是那一个个圈),那么这些圈的边沿就构成了等值线/等高线。
当你在山区中沿着山的表面向各个方搜索山谷的最低点时,你走动的轨迹投影在地面上,就会形成图中的那些“搜索方向”。
当然,必须要明确的一点是:我们只拿三维空间来作比喻,也就是我们可以想像出来的现实世界的例子。但是在数学问题中,通常有更高的维度(例如10万维的空间),这个时候,我们无法像三维立体投影到二维平面一样作出形象的比喻,因此,要理解等值线/等高线,只需要拿三维空间和二维平面来理解就行了。
(9)为什么最优化问题总是和“凸函数”(convex function) 扯上关系
凸函数的定义请看这里。凸函数的几何意义(在二维平面上)为:f(x)上任意两点间的弦始终位于两点间弧的上方。
但凡是本最优化的书,几乎都会提到凸函数,这是因为最优化问题基本上都是在“目标函数为凸函数”的前提下来讨论的——我不知道“基本上”一词用得正确与否,但是就我看过的一些内容说,它们都会这样假设。
因此,要把最优化算法应用在你的工程实际中,你先要判断你的目标函数是不是凸函数,因为这是个基础条件。当然,如果要靠凸函数的定义来判断目标函数是不是凸函数,在实际中就比较难了,通常都是用目标函数的梯度(一阶导数)或二阶导数(Hesse矩阵)来判断,人们已经得到了很多定理,例如在定义域内任一点上目标函数的Hesse矩阵半正定,则其为凸函数。利用这些定理,可以比使用凸函数的定义更容易判断。
(10)一维搜索方法和信赖域方法的关系
一维搜索方法,又叫线搜索(line search)方法,它与信赖域(trust region)方法都是最优化算法领域的基础方法,所谓基础方法,是指它们是很多最优化算法的一个组成部分。例如,DFP算法中会用到一维搜索方法,LM算法中会用到信赖域方法。最优化算法要么会使用一维搜索方法,要么会用到信赖域方法,总之,二选一。因此,可以把一维搜索方法和信赖域方法看成一种平等的关系,它们就像建造一栋大楼所需的两种材料A和B,你可以用A,或者用B。
文章来源:https://www.codelast.com/
➤➤ 版权声明 ➤➤
转载需注明出处:codelast.com
感谢关注我的微信公众号(微信扫一扫):
